用 PyTorch 写一个 NanoGPT (2): MultiheadAttention 模块以及 RoPE 相对位置编码

仓库链接: https://github.com/Davidwadesmith/NanoGPT

本项目参照 NanoGPT，实现了一个简单易用的 GPT 语言模型。适合用于学习和实验生成式预训练变换器 (GPT) 的核心原理。

概览

上期说到，在 Attention is all you need 这篇文章中还有一部分多头注意力的实现：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
q = torch.transpose(
    q.view(
        self.cfg.batch_size,
        self.cfg.seqlen,
        self.cfg.head_n,
        self.cfg.hidden_dim // self.cfg.head_n,
    ),
    1,
    2,
)  # (batch_size, head_n, seqlen, head_dim)

k = torch.transpose(
    k.view(
        self.cfg.batch_size,
        self.cfg.seqlen,
        self.cfg.head_n,
        self.cfg.hidden_dim // self.cfg.head_n,
    ),
    1,
    2,
)  # (batch_size, head_n, seqlen, head_dim)

v = torch.transpose(
    self.wv(hidden_tokens).view(
        self.cfg.batch_size,
        self.cfg.seqlen,
        self.cfg.head_n,
        self.cfg.hidden_dim // self.cfg.head_n,
    ),
    1,
    2,
)  # (batch_size, head_n, seqlen, head_dim)

可以看到其实并不是很难的操作，只是把所有矩阵进行变换操作。之所以不用循环是因为 Python 中循环实在是慢，把多头合并成一个矩阵其实是将这个循环操作移交给底层的 C 库进行，这就快得多了。

回顾一下具体的公式：

$$ \begin{aligned} \text{MultiHead}(Q,K,V) &= \text{Concat}(\text{head}_1,...,\text{head}_\mathrm{h})W^O \\ \text{where head}_\mathrm{i} &= \text{Attention}(QW_i^Q, KW_i^K, VW_i^V) \end{aligned} $$

实际操作的时候我们只是把 hidden_dim 拆成 $n$ 个 head_dim，这个操作使用 view 其实很简单。然后 head 的数量这一维其实就没有参与矩阵运算了，所以我们用转置把它移到前面去和 batch_size 待到一块。经过这样的处理就能并行计算多个 head 了。

但是还要注意最后还要接一个全连接，其实这里的解释性我感觉不强，但是抛开理论不谈，这里单纯只是一个恢复原来形状然后接一个线性层的事：

1
2
3
4
5
return self.wo(
    torch.transpose(masked_attention, 1, 2).reshape(
        self.cfg.batch_size, self.cfg.seqlen, self.cfg.hidden_dim
    )
)  # (batch_size, seqlen, hidden_dim)

这个就是加了 Multihead 的 Attention 模块，用最小的改动得到了最大的效果。

RoPE 位置编码

位置编码有很多种，sinusoidal 编码、可学习线性层编码，或者 RoPE 编码。现在多用 RoPE 编码，原因在于它可以拓展上下文长度，比如训练时固定取前面 $n$ 个 token 作为上下文，训练出来的模型我拿更长的上下文推理也可以跑得很好。

其他编码比如 sinusoidal 也可以，但是没 RoPE 好，而可学习线性层则是只能定长上下文窗口，所以我们选择 RoPE。而这个编码需要在 MultiheadAttention 内部实现，对 $K$ 和 $Q$ 进行编码。

RoPE 的原理在于，我们认为一个 token 经过线性层得到的对应的 $K_i, Q_i, V_i$，应该是 $i$ 的函数，也是原来的 token 的函数：

$$ \begin{aligned} \boldsymbol{q}_m &= f_q(\boldsymbol{x}_m,m) \\ \boldsymbol{k}_n &= f_k(\boldsymbol{x}_n,n) \\ \boldsymbol{v}_n &= f_v(\boldsymbol{x}_n,n) \end{aligned}$$

而我们后面的得到的 Attention score (或者说 weight)，则是一个与 $m, n$ 都有关的函数，最终的输出则是一个和 $m$ 有关的函数：

$$ \begin{aligned} a_{m,n} &= \frac{\exp(\frac{\boldsymbol{q}_m^\intercal\boldsymbol{k}_n}{\sqrt{d}})}{\sum_{j=1}^N\exp(\frac{\boldsymbol{q}_m^\intercal\boldsymbol{k}_j}{\sqrt{d}})} \\ \mathbf{o}_m &= \sum_{n=1}^N a_{m,n}\boldsymbol{v}_n \end{aligned} $$

RoPE 的思路是这样的，对于 $a_{m,n}$ 来说，我们希望它只体现出 $m$ 位置和 $n$ 位置的距离，我们不希望 $m$ 和 $n$ 具体在哪里对 $a$ 的值有影响。因此我们希望这是一个关于 $m-n$ 的函数。鉴于计算 Attention score 的时候有点积，我们希望：

$$ \langle f_q(\boldsymbol{x}_m,m), f_k(\boldsymbol{x}_n,n)\rangle = g(\boldsymbol{x}_m, \boldsymbol{x}_n, m-n) $$

这种乘运算变加减运算的特征让我们想起指数函数，因此构造：

$$ \begin{aligned} f_q(\boldsymbol{x}_m,m) &= (\boldsymbol{W}_q\boldsymbol{x}_m)e^{im\theta} \\ f_k(\boldsymbol{x}_n,n) &= (\boldsymbol{W}_k\boldsymbol{x}_n)e^{in\theta} \\ g(\boldsymbol{x}_m, \boldsymbol{x}_n, m-n) &= \mathrm{Re}[(\boldsymbol{W}_q\boldsymbol{x}_m)(\boldsymbol{W}_k\boldsymbol{x}_n)^*e^{i(m-n)\theta}] \end{aligned} $$

在数学上，这等价于在得到 $q$ 和 $k$ 后把它俩进行不同程度的旋转，即左乘一个旋转矩阵：

$$f_{\{q,k\}}(\boldsymbol{x}_m,m) = \begin{pmatrix} \cos m\theta & -\sin m\theta \\ \sin m\theta & \cos m\theta \end{pmatrix} \begin{pmatrix} W_{\{q,k\}}^{(11)} & W_{\{q,k\}}^{(12)} \\ W_{\{q,k\}}^{(21)} & W_{\{q,k\}}^{(22)} \end{pmatrix} \begin{pmatrix} x_m^{(1)} \\ x_m^{(2)} \end{pmatrix}$$

这里 ${q, k}$ 的意思是这里能填 $q$ 也能填 $k$。

这只是一个 hidden_dim 为 2 的情况，但是扩展一下，一般的 hidden_dim 都很大，而这样所对应的旋转矩阵就会是一个 hidden_dim * hidden_dim 大小的巨大的稠密矩阵，计算量增加很多。

因此我们不进行高维的旋转，而是每两个维度凑一起来旋转，这样等价于每次只在一个高维空间内的二维子空间上旋转，所得到的旋转矩阵变成了稀疏矩阵。虽然维度还是很大，但是对于这种稀疏矩阵我们有特别的方法计算：

$$ \boldsymbol{R}_{\Theta,m}^d = \begin{pmatrix} \cos m\theta_1 & -\sin m\theta_1 & 0 & 0 & \cdots & 0 & 0 \\ \sin m\theta_1 & \cos m\theta_1 & 0 & 0 & \cdots & 0 & 0 \\ 0 & 0 & \cos m\theta_2 & -\sin m\theta_2 & \cdots & 0 & 0 \\ 0 & 0 & \sin m\theta_2 & \cdots & 0 & 0 \\ \vdots & \vdots & \vdots & \vdots & \ddots & \vdots & \vdots \\ 0 & 0 & 0 & 0 & \cdots & \cos m\theta_{d/2} & -\sin m\theta_{d/2} \\ 0 & 0 & 0 & 0 & \cdots & \sin m\theta_{d/2} & \cos m\theta_{d/2} \end{pmatrix} $$

可以注意到，$x$ 与这个矩阵相乘，每个元素只会被计算两次，奇数的会乘 $\cos m\theta$ 和 $\sin m\theta$，而偶数位置上的元素会乘 $-\sin m\theta$ 和 $\cos m\theta$。

你可能会认为我们要挑奇数位置上的元素乘 $\cos$ 然后减去偶数位置上的元素乘 $\sin$ 来得到结果中奇数位置上的东西，结果中偶数位置上的东西同理。但其实比这还可以更简单一点，一个重要的洞见在于，我们从来没说好要相邻的元素才能凑一对旋转。实际上，我们完全可以把要乘 $\cos$ 的位置给前面一半的元素，而乘 $\sin$ 的给后面一半的元素，这样更简洁同时也让数据更连续了：

1
2
3
4
5
6
7
8
9
10
11
12
13
result = torch.zeros_like(x).to(device)  # (batch_size, seqlen, hidden_dim)

# ...对pe进行处理...

result[:, :, : hidden_dim // 2] = x[:, :, : hidden_dim // 2] * torch.cos(
    pe * position
) - x[:, :, hidden_dim // 2 :] * torch.sin(pe * position)

result[:, :, hidden_dim // 2 :] = x[:, :, : hidden_dim // 2] * torch.sin(
    pe * position
) + x[:, :, hidden_dim // 2 :] * torch.cos(pe * position)

return result

可以看到有个 pe 变量，这个其实就是在回答刚才没说的问题，也就是 $\theta_i$ 怎么来的，以及它和 $i$ 的关系。

其实在我们刚才的推导中，$\theta_i$ 只是凑的那两个维度构成的平面上 $x$ 旋转的角度，理论上来说这些 theta 可以任意设，全都一样都没问题。不过 RoPE 从 sinusoidal 位置编码中汲取了灵感，让一部分维度旋转多一些，一部分旋转少一些：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
position = (
    torch.arange(0, seqlen, dtype=torch.float32).unsqueeze(1).unsqueeze(0)
).to(
    device
)  # (1, seqlen, 1)

pe = (
    torch.exp(
        (-torch.arange(0, hidden_dim, 2, dtype=torch.float32))
        / hidden_dim
        * torch.log(torch.tensor(10000.0))
    )
    .unsqueeze(0)
    .unsqueeze(0)
).to(
    device
)  # (1, 1, d // 2)

这个遵循公式：

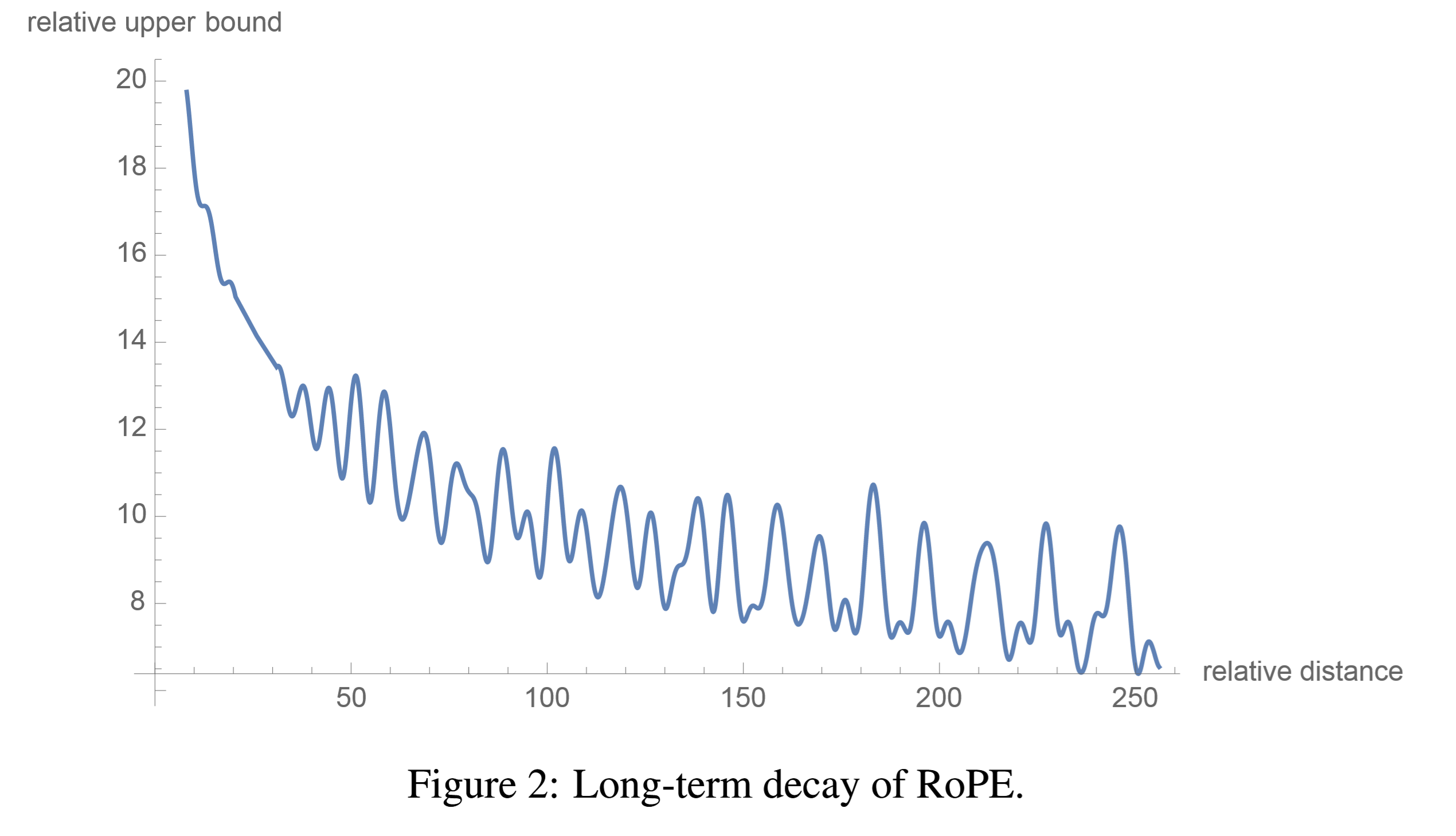
但是注意两个位置编码使用这个思想的目的不一样，sinusoidal 必须用这种方法来区别开不同的位置，而 RoPE 使用这个 idea 是为了 Long-term decay，它使得长距离的 token 的 $q, k$ 点积的值减小，这在论文中得到了证明（虽然用的方法不太显然）。这里只是贴一下论文中的思路：

详细证明

image-20251218220126328

3.4.3 Long-term decay of RoPE

We can group entries of vectors $\boldsymbol{q} = \boldsymbol{W}_q \boldsymbol{x}_m$ and $\boldsymbol{k} = \boldsymbol{W}_k \boldsymbol{x}_n$ in pairs, and the inner product of RoPE in Equation (16) can be written as a complex number multiplication:

where $\boldsymbol{q}{[2i:2i+1]}$ represents the $2i^{th}$ to $(2i+1)^{th}$ entries of $\boldsymbol{q}$. Denote $h_i = \boldsymbol{q}{[2i:2i+1]} \boldsymbol{k}{[2i:2i+1]}^*$ and $S_j = \sum{i=0}^{j-1} e^{i(m-n)\thetai}$, and let $h{d/2} = 0$ and $S_0 = 0$, we can rewrite the summation using Abel transformation:

Thus,

Note that the value of $\frac{1}{d/2} \sum_{i=1}^{d/2} |S_i|$ decay with the relative distance $m - n$ increases by setting $\theta_i = 10000^{-2i/d}$, as shown in Figure (2).

总结

其实 MultiheadAttention 不难，RoPE 需要理解一下，总的来说还好。

下一期说归一化和残差连接。